Trees are data structures made out of a root node connected to subtrees called child nodes. Trees are a type of graph.

Below is a visualization of a labeled tree.

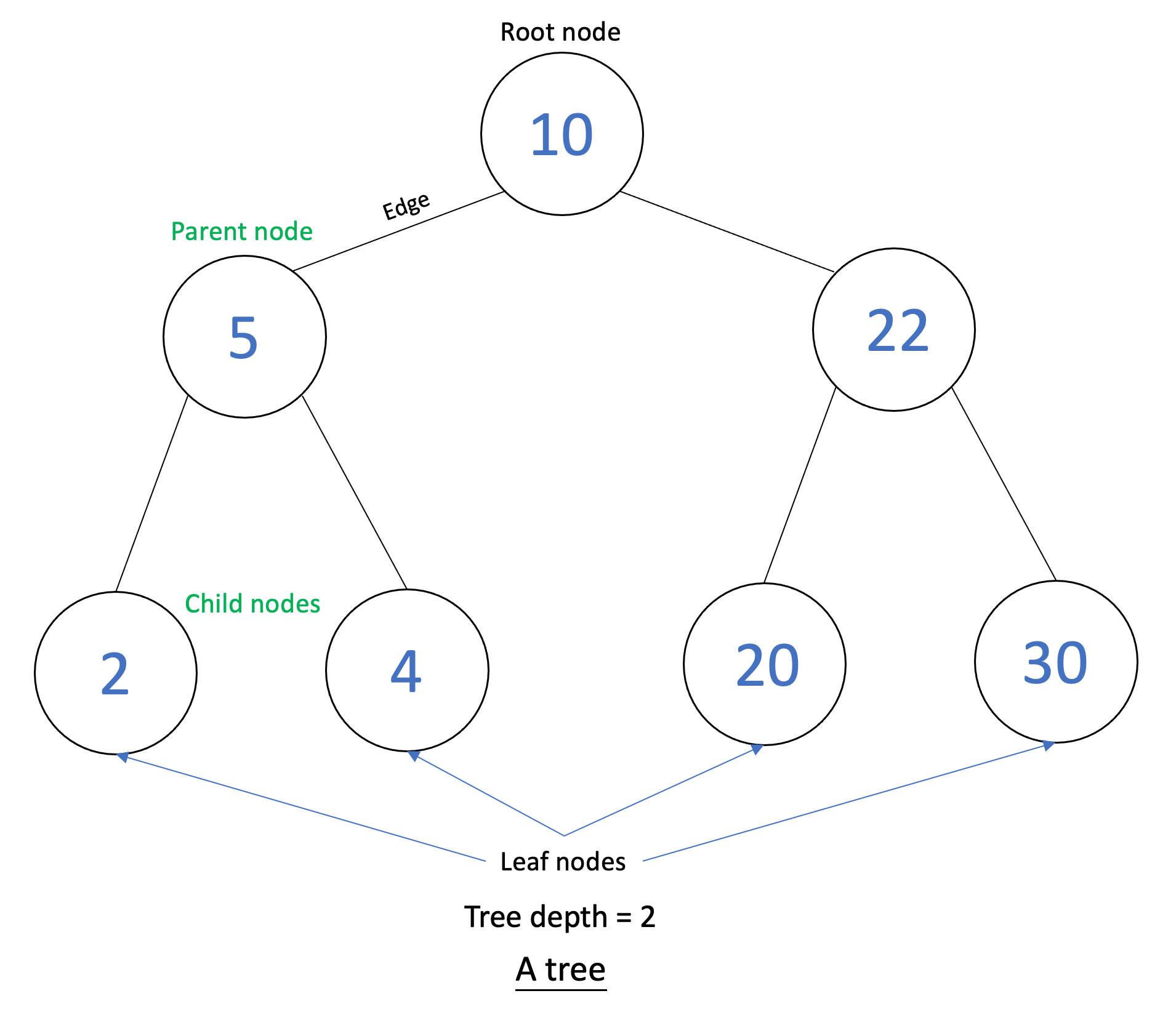
Tree Terminology

• Node: An object that stores data and links/pointers to child nodes.
• Root node: The first node in a tree.
• Edge: A link between two nodes.
• Child node: A node pointed to by a parent node.
• Parent node: A node that has one or more child nodes.
• Leaf node: The last node in a path. Leaf nodes have no children.
• Height of a node: The number of edges between that node and the furthest leaf node.
• Depth of a node: The number of edges between that node and the root node.
• Depth of a tree: The number of edges between the root node and the furthest leaf node.

Types of Trees

• Binary trees: Trees where each node has less than or equal to 2 child nodes.
• Binary search trees: A binary tree optimized for binary search. Each node’s left child has a value less than the current node, and its right child has a value greater than the current node.
• Tries: A tree that contains characters. Useful for storing dictionaries of words.

Tree Traversal

There are three main methods for tree traversal: pre-order, in-order, and post-order traversal. The main difference between each method is when the root node is visited.

Pre-order traversal

Here, the root node is visited first, hence the name pre-order traversal.

Steps:

1. Visit the root node.
2. Visit the left subtree.
3. Visit the right subtree.

This recursive Python function prints a binary tree via pre-order traversal:

For the other traversal methods, we rearrange the order of the lines of code in the if statement.

In-order traversal

Steps:

1. Visit the left subtree.
2. Visit the root node.
3. Visit the right subtree.

Post-order traversal

Steps:

1. Visit the left subtree.
2. Visit the right subtree.
3. Visit the root node.

Time Complexity

Tree traversal time complexity: \(O(n)\)

More Resources

Below are some more resources to learn about trees:

Programiz - Tree Data Structure

GeeksforGeeks - Binary Tree Data Structure

YouTube - Trees by HackerRank