Quicksort
Quicksort is a recursive sorting algorithm that works by sorting array elements around a pivot. This process repeats until the array is sorted.
Functions
Quicksort uses two main functions:
- Partition: This function selects a “pivot value”. All elements less than the pivot value are moved before it, and all elements larger than the pivot value are moved after it in the array. The function then returns the pivot value.
- Quicksort: This function partitions the array, then calls itself on the array elements before and after the pivot value.
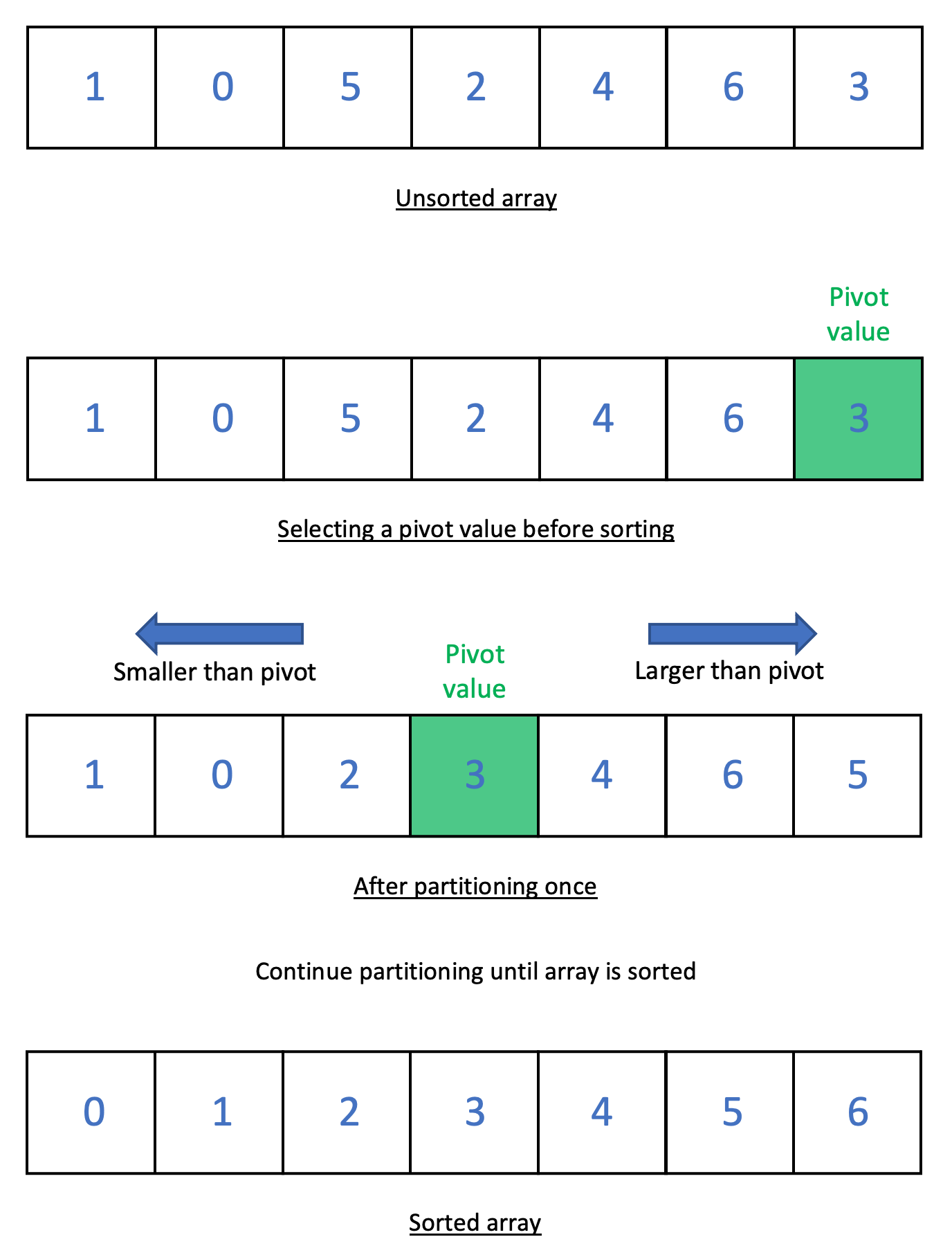
Choosing the Pivot Value
How the pivot value is chosen ultimately affects the Quicksort’s time complexity.
Oftentimes, the first element or last element is always chosen as the pivot value. However, for sorted arrays, this can lead to \(O(n^2)\) time complexity. This is because the largest or smallest element in the array is chosen as the pivot. When the array is partitioned, one half has no elements, while the other half has \(n-1\) elements.
The best-case runtime happens when the median is chosen every time as the pivot. Choosing the median as the pivot divides the array into two equal halves, resulting in \(O (n \ log \ n)\) runtime.
If the pivot is chosen randomly, this will result in average \(O (n \ log \ n)\) runtime. Choosing the largest or smallest element each time now becomes exceedingly rare. This means that while \(O(n^2)\) runtime is possible, it is very unlikely.
Another method is to select three random array elements and use the median of the three values as the pivot value. This ensures that the largest or smallest element is never chosen, but more comparisons are made in order to choose the pivot.
Partition Function Steps
Suppose we have an array \(A\) that we want to partition. For simplicity, we will choose the last array element as the pivot each time.
Steps for the partition function:
- Pass an array \(A\), the low index, and the high index into the partition function. The indices determine the search space for the function.
- Choose the last element of the array as the pivot value.
- Create a variable \(i\) and set it equal to the low index.
- Use a for loop and a counter variable \(j\) to scan through the entire array. \(j\) starts at the low index and is incremented until it reaches the high index.
- If \(A[j]\) is less than the pivot value, swap it with \(A[i]\) and increment \(i\) by 1. This step moves smaller elements to the front of the array.
- When the for loop finishes, swap \(A[i]\) with \(A[high \ index]\). This step puts the pivot value in the right spot in the array. All elements greater than the pivot value are not after it in the array.
- \(i\) now marks the index location of the pivot value. Return \(i\).
Quicksort Function Steps
Steps for quicksort:
- Pass the array, the lowest index, and highest index of the array into the quicksort function.
- Move onto step 3 only if the low index is less than the high index. Otherwise, do nothing. This is the base case.
- Call the partition function. The return value will be the pivot index.
- Call quicksort on all elements before the pivot index.
- Call quicksort on all elements after the pivot index.
Time Complexity
Partition function time complexity: \(O(n)\)
Quicksort average time complexity: \(O(n \ log \ n)\)
Quicksort worst-case time complexity: \(O(n^2)\)
More Resources
Below are some more resources to learn about quicksort:
YouTube - Quicksort by HackerRank
YouTube - The Quicksort Sorting Algorithm by Back to Back SWE