Heaps are complete binary trees where the root node is larger than or smaller than the child nodes, depending on the heap’s type. Heapsort uses this property to sort arrays.

Types of Heaps

There are two types of heaps:

• In max heaps, the root node is larger than the child nodes.
• In min heaps, the root node is smaller than the child nodes.

This heap property must be maintained for all child nodes. So for a max heap, the children of the root node must also be max heaps.

Example Heaps

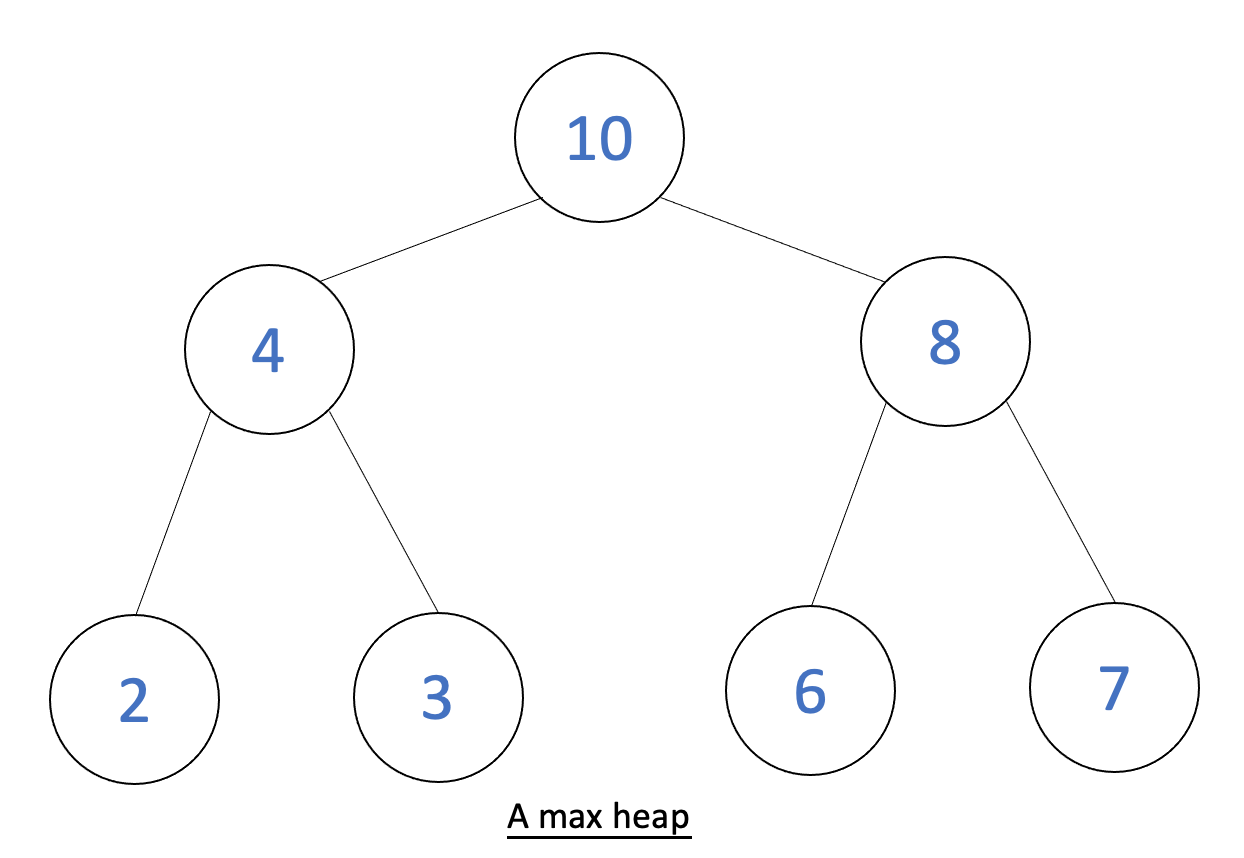
Below is a picture of a max heap:

Representing Heaps as Arrays

Suppose we want to store the above heap as an array, called \(A\). The size of \(A\) is \(n\).

We can represent a heap as an array if we follow these rules:

• The root node of the heap is \(A[0]\)
• The parent of a node with index \(i\) is at index \(\lfloor \frac{i}{2} \rfloor \)
• The left child of index \(i\) is at index \(2i+1\)
• The right child of index \(i\) is at index \(2i+2\)
• The index of the last non-leaf node is at index \(\frac{n}{2} - 1\)

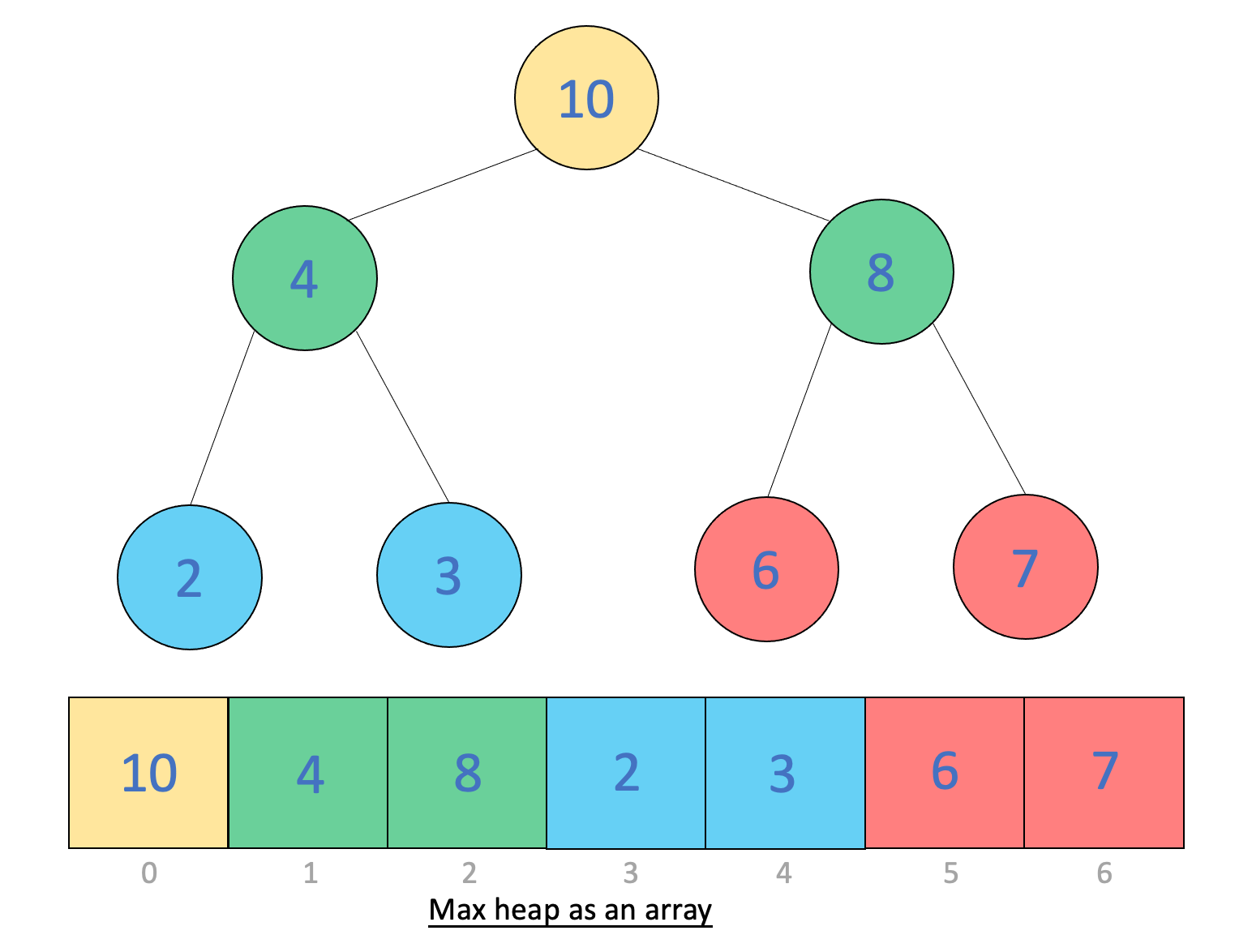
The largest value in a max heap is always the first array element, or \(A[0]\). For a min heap, the smallest value is at \(A[0]\).

This will work for both max heaps and min heaps. We’ll use these properties when heapifying the array.

Heap Functions

Below are functions needed to heapsort an array. Suppose we have an array \(A\) that we want to use heapsort on.

Heapify

The heapify function maintains the heap property in a heap. For max heaps, this means swapping heap values until all parent nodes are larger than their children.

Steps for a max heapify function:

1. Create a function that takes an array, its size, and an index \(i\) as parameters.
2. Create a variable called \(largestIndex\) and set it equal to \(i\). This keeps track of the largest element.
3. Create a \(leftIndex\) variable and set it to \(2i+1\).
4. Create a \(rightIndex\) variable and set it to \(2i+2\).
5. If \(A[leftIndex]\) or \(A[rightIndex]\) is larger than \(A[largestIndex]\), set \(largestIndex\) to the index of the new largest value.
6. If \(largestIndex\) does not equal \(i\):
   • Swap \(A[i]\) and \(A[largestIndex]\)
   • Call max heapify on array \(A\) at index \(largestIndex\)

Build max heap

This function converts an array into a max heap.

Steps:

1. Let index \(i = \frac{n}{2} - 1\) and \(n\) be the size of \(A\).
2. Call heapify on \(A[i]\).
3. Subtract \(i\) by \(1\).
4. Repeat steps 2-3 until \(i\) equals \(-1\).

Heapsort in ascending order

This function sorts an array in ascending order using max heaps.

Steps:

1. Let \(n\) be the size of \(A\).
2. Call build max heap on \(A\).
3. Since \(A[0]\) is the largest value, we swap the first and last array elements to move the largest value to the end.
4. Subtract \(n\) by \(1\) since the last array element is already sorted.
5. Call heapify on \(A[0]\) to make the next largest element the root node.
6. Repeat steps 2-5 until \(n\) equals \(0\).

Time Complexity

Heapify time complexity: \(O(log \ n)\)

Build max heap time complexity: \(O(n)\)

Heapsort time complexity: \(O(n \ log \ n)\)

More Resources

Below are some more resources to learn about heaps and heapsort:

GeeksforGeeks - Heap Data Structure

GeeksforGeeks - HeapSort