Graphs can be searched in two main ways: depth-first search (DFS) and breadth-first search (BFS).

Depth-First Search (DFS)

Depth-first search traverses a graph by going deep into a chain of nodes before visiting other chains. DFS visits all of the children before visiting adjacent nodes. This happens until the graph has been fully explored. DFS is implemented with a stack.

Below is an image of how DFS goes through a graph. DFS traverses the nodes 1 through 7 in order.

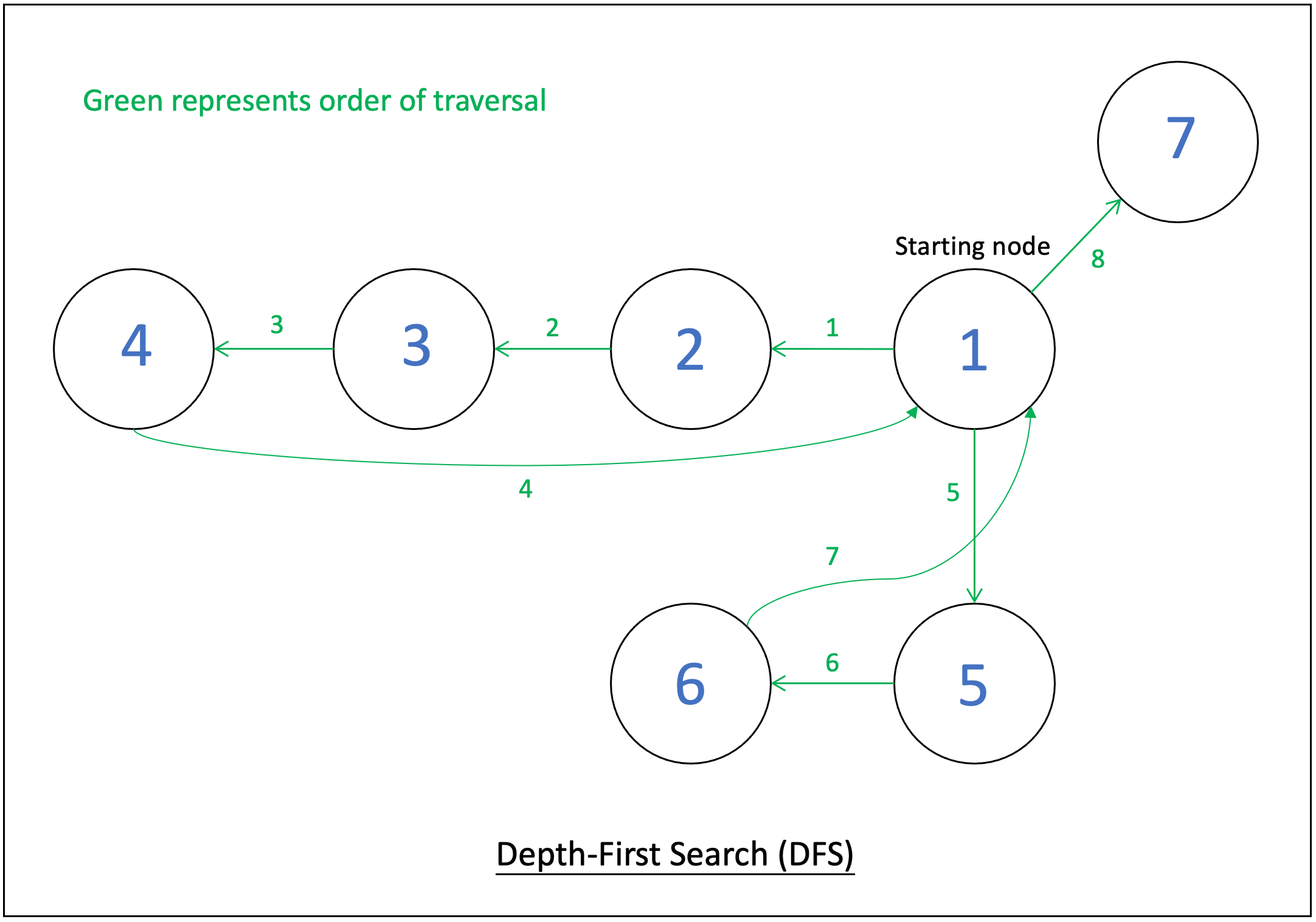
DFS can be implemented recursively or iteratively. Below are the algorithms for both methods. The algorithms below use a graph implemented with an adjacency list.

Iterative Algorithm

1. Pass a graph node into the DFS function.
2. Create a stack. This stack stores nodes that still need to be processed.
3. Create a list that stores whether each node has been visited yet. At this point, all of the nodes are marked as not visited.
4. Push the first node to the stack.
5. While the stack is not empty:
   1. Pop the last node put in.
   2. If the popped node has not been visited, visit it and mark it as visited in the list.
   3. Create a for loop to push each node’s adjacent nodes to the stack.

Recursive Algorithm

1. Pass the graph, the current node, and a list storing the visited status of each node into the DFS function.
2. Mark the current node as visited.
3. Visit the current node.
4. Create a for loop to check all of the current node’s adjacent nodes.
   1. If the adjacent node has not been visited yet, call DFS on that node.

Breadth-First Search (BFS)

Breadth-first search goes wide rather than deep, visiting nodes level by level. BFS explores a node’s neighbors before exploring the rest of the graph. BFS is implemented with a queue. Unlike DFS, BFS can only be implemented iteratively.

Below is an image of how BFS goes through a graph. BFS traverses the nodes one level out, then two levels out, then three levels out.

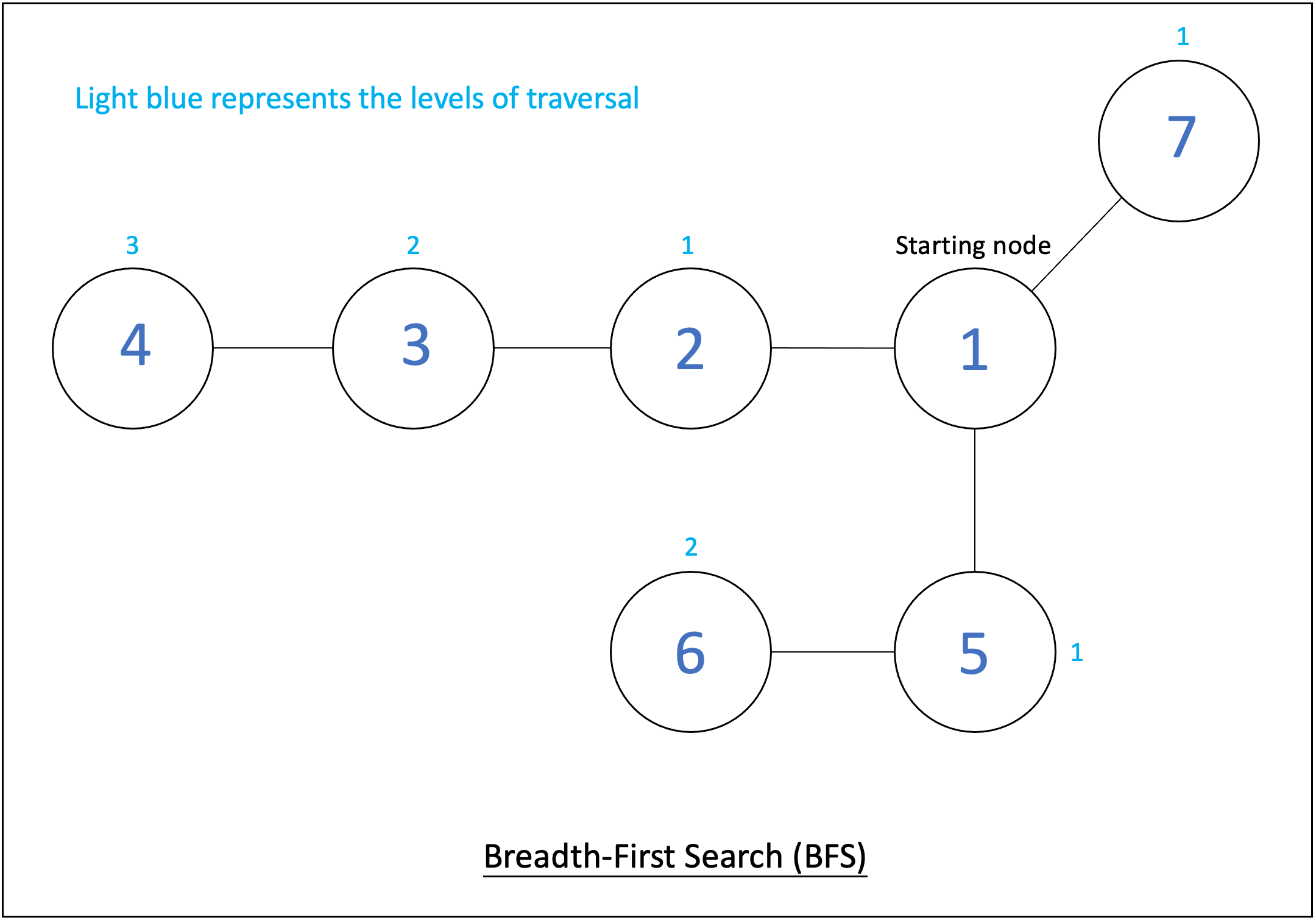
We go out level by level, visiting the first node, then the nodes in the next level, and then the next level, until all of the nodes have been visited. If we were to print the nodes via BFS, we would print 1, then 7,5, and 2, then 6 and 3, and then 4.

Algorithm

This algorithm uses a graph implemented with an adjacency list.

1. Pass the graph node into the BFS function.
2. Create a queue to store the items that need to be processed.
3. Create a list to store the items that have already been processed.
4. Add the node to the queue.
5. While the queue is not empty:
   1. Pop the first item in the queue.
   2. If the popped node is not in the processed list:
      1. Add it to the processed list.
      2. Visit the popped node.
   3. Use a for loop to go through the popped node’s adjacent nodes.
      1. If the for loop reaches a node that hasn’t been processed yet, add it to the queue.

Complexity

Time complexity for both algorithms: \(O(V + E)\)

Space complexity for both algorithms: \(O(V)\)

where \(V = number \ of \ vertices\)

\(E = number \ of \ edges\)

More Resources

Below are some more resources to learn about graph search:

GeeksforGeeks - Depth First Search or DFS for a Graph

GeeksforGeeks - Breadth First Search or BFS for a Graph

YouTube - Graph Search, DFS and BFS by HackerRank