Big O (big-oh) notation gives computer scientists a way to show a program’s time complexity.

Basics of Big O

Time complexity is the time it takes to run a program. Big O is the notation used to represent time complexity as the program’s input size increases.

Finding a Program’s Time Complexity

Example 1

To find a program’s big O complexity, we need to accomplish the following tasks:

1. Find the big O complexity of each line and add them all up.
2. Ignore any constants and any terms that aren’t dominant.

For example, look at the following two lines of C code:

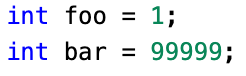
1. Assigning values to variables takes constant time. This means that no matter how large the value is, assigning it to a variable takes the same amount of time. In Big O terms, constant time is \(O(1)\) (pronounced big-oh of one). Because both lines are O(1), adding \(O(1) + O(1) = O(2)\).
2. We can actually simplify \(O(2)\) by treating 2 as a constant: \(O(2) = O(2 \bullet 1)\). Because we remove the constant, this simplifies down to \(O(1)\). We only have one term, so there is no need to worry about non-dominant terms.

After following these steps, we find that the Big O complexity is \(O(1)\).

Example 2

Let’s find the time complexity of the following lines of code, which finds the sum of a 1D array:

1. The first two lines are declaration/assignment statements, so they both take \(O(1)\) time.
   Likewise, the code in the while loop takes \(O(1)\) time since addition takes constant time.
   However, the while loop itself runs n times, depending on the size of the array. This means the time complexity for the while loop is \(O(n)\).
2. We combine all of step one as follows: \(O(1) + O(1) + O(n) \times (O(1) + O(1))\).
   Because we ignore non-dominant terms, we can safely ignore each \(O(1)\). Now, the time complexity is \(O(n)\).

Our final answer is \(O(n)\).

Example Complexities

Below is a list of example runtimes and how to represent them in Big O:

Runtime	Big O Notation	Example Algorithm
Constant time	\(O(1)\)	Accessing an array element
Linear time	\(O(n)\)	Finding the sum of an 1D array
Quadratic time	\(O(n^2)\)	Finding the sum of a 2D array
Logarithmic time	\(O(log(n))\)	Using binary search

More Resources

Below are some more resources to learn about Big O Notation:

Big O Cheat Sheet

YouTube - Big-O Notation in 5 minutes by Michael Sambol